The Most Comprehensive Large Model Dataset Sharing: Part 1, Mathematics Datasets

Currently, large models still have significant room for improvement in the field of mathematics, and the foundation for training their mathematical capabilities lies in high-quality mathematical datasets. Below, we will introduce some open-source mathematical datasets.

GSM8K

https://huggingface.co/datasets/openai/gsm8k

{'question': 'Natalia sold clips to 48 of her friends in April, and then she sold half as many clips in May. How many clips did Natalia sell altogether in April and May?','answer': 'Natalia sold 48/2 = <<48/2=24>>24 clips in May.\nNatalia sold 48+24 = <<48+24=72>>72 clips altogether in April and May.\n#### 72',}

The GSM8K dataset is one of the common benchmarks for evaluating the mathematical capabilities of large models. The GSM8K dataset consists of 8.5K high-quality, linguistically diverse elementary and middle school math word problems. Its key feature lies in providing a large number of problems, each accompanied by a natural language solution. The primary application of this dataset is to support the diagnosis of current models' reasoning deficiencies and help drive progress in related research. Through GSM8K, researchers can test and improve model performance in multi-step mathematical reasoning tasks, especially in scenarios requiring complex reasoning. GSM8K serves as an effective benchmark for assessing and enhancing model performance.

MATH

https://github.com/hendrycks/math

{"problem": "Let $$\\mathbf{a}$$ and $$\\mathbf{b}$$ be vectors such that\n\\[\\mathbf{v} = \\operatorname{proj}_{\\mathbf{a}} \\mathbf{v} + \\operatorname{proj}_{\\mathbf{b}} \\mathbf{v}\\]for all vectors $$\\mathbf{v}.$$  Enter all possible values of $$\\mathbf{a} \\cdot \\mathbf{b},$$ separated by commas.","level": "Level 4","type": "Precalculus","solution": "Taking $$\\mathbf{v} = \\mathbf{b},$$ we get\n\\[\\mathbf{b} = \\operatorname{proj}_{\\mathbf{a}} \\mathbf{b} + \\operatorname{proj}_{\\mathbf{b}} \\mathbf{b}.\\]From the projection formula,\n\\[\\operatorname{proj}_{\\mathbf{a}} \\mathbf{b} = \\frac{\\mathbf{a} \\cdot \\mathbf{b}}{\\|\\mathbf{a}\\|^2} \\mathbf{a},\\]and $$\\operatorname{proj}_{\\mathbf{b}} \\mathbf{b} = \\mathbf{b},$$ so\n\\[\\mathbf{b} = \\frac{\\mathbf{a} \\cdot \\mathbf{b}}{\\|\\mathbf{a}\\|^2} \\mathbf{a} + \\mathbf{b}.\\]Hence,\n\\[\\frac{\\mathbf{a} \\cdot \\mathbf{b}}{\\|\\mathbf{a}\\|^2} \\mathbf{a} = \\mathbf{0}.\\]The vector $$\\mathbf{a}$$ must be nonzero, in order for the projection of $$\\mathbf{v}$$ onto $$\\mathbf{a}$$ to be defined, so we must have $\\mathbf{a} \\cdot \\mathbf{b} = \\boxed{0}.$\n\nNote that we can take $$\\mathbf{a} = \\begin{pmatrix} 1 \\\\ 0 \\end{pmatrix}$$ and $\\mathbf{b} = \\begin{pmatrix} 0 \\\\ 1 \\end{pmatrix}.$"}

The MATH dataset consists of 12,500 complex math competition problems, covering various branches of mathematics such as algebra, geometry, probability, and number theory. A notable feature of this dataset is that each problem comes with detailed step-by-step solutions. This allows it to not only test the ability of machine learning models to find the correct answers but also evaluate their capability to generate logical reasoning and problem-solving processes. Since the difficulty of the problems matches that of math competitions, this dataset is highly challenging and suitable for advancing and validating advanced mathematical problem-solving techniques. Additionally, the step-by-step solutions in the dataset provide a rich resource for automated evaluation and model training, contributing to the further development of machine learning algorithms in the field of mathematics.

Orca-Math-200K

https://huggingface.co/datasets/microsoft/orca-math-word-problems-200k

{"question":"A is 3 groups of 10 and 7 individual units, and B is the number obtained by subtracting 1 from 40. Which is smaller, A or B?","answer":"Let's calculate the value of A and B. A is 3 groups of 10 and 7 individual units. So, A = (3 * 10) + 7 = 30 + 7 = 37. B is the number obtained by subtracting 1 from 40. So, B = 40 - 1 = 39. Now, we compare A and B. A = 37 B = 39 Since 37 is less than 39, A is smaller than B."}

The Orca-Math-200K dataset is a large-scale synthetic math problem collection containing 200,000 math word problems. This dataset is primarily used for training and evaluating the capabilities of language models in solving mathematical problems. It offers a range of diverse math problems, from easy to difficult, to challenge and enhance the reasoning and problem-solving skills of models. The dataset's generation process involves collecting initial seed problems and using collaborative agents to rephrase and create new problems, thereby enriching the diversity and difficulty of the problem set. This process not only improves the quality of the dataset but also provides more possibilities and flexibility for model training, helping to effectively enhance model performance in the field of mathematics while ensuring data freshness and diversity.

NaturalProofs

https://github.com/wellecks/naturalproofs

{"id": 30777,"type": "definition","label": "Definition:Folium of Descartes/Cartesian Form","title": "Definition:Folium of Descartes/Cartesian Form","categories": ["Definitions/Folium of Descartes"],"contents": ["The '''folium of Descartes''' is the [[Definition:Locus|locus]] of the [[Definition:Equation of Geometric Figure|equation]]:",":$x^3 + y^3 - 3 a x y = 0$"],"refs": ["Definition:Locus","Definition:Equation of Geometric Figure"],"ref_ids": [22165,25822],"proofs": []},

NaturalProofs shifts from basic computation and applied problems to more abstract and theoretical mathematical proofs. NaturalProofs is a large-scale formal mathematical proof dataset, consisting of 32k theorem statements and proofs, 14k definitions, and 2k other types of pages (e.g., axioms, corollaries). These pages are sourced from three domains: ProofWiki, an online compilation of mathematical proofs written by a community of contributors; the Stacks Project, a web-based algebraic and geometric textbook; and data from mathematical textbooks. The emergence of NaturalProofs provides a valuable resource for researching the capabilities of artificial intelligence in advanced mathematical reasoning and proof generation. It not only challenges the logical reasoning abilities of large models but also tests their capacity to understand and generate human-readable mathematical proofs. The scale and quality of this dataset make it an important benchmark for evaluating and improving the performance of large models in advanced mathematics.

LeanDojo

https://github.com/lean-dojo/LeanDojo

LeanDojo is a resource specifically designed for learning-based theorem provers, extracting a large amount of training data from the mathematical library of the Lean programming language. This dataset contains 98,734 theorems and their proofs, as well as 130,262 definitions of premises, making it one of the largest datasets in the field of theorem proving. Theorem proving is a core task for machine learning in formal mathematics and verification, and the LeanDojo dataset is constructed to provide a rich resource for training and evaluating automated theorem proving systems.

The construction process of the LeanDojo dataset employs program analysis techniques to ensure data quality and relevance, particularly in premise selection, which is a critical bottleneck in theorem proving. By providing finely annotated proof premises, the dataset supports the training and evaluation of premise selection. Additionally, the LeanDojo dataset introduces a novel split strategy called "novel_premises split," which requires that proofs in the test set must use at least one premise not seen in the training set. This helps prevent models from over-relying on memorizing training data, thereby enhancing their generalization capabilities.

LeanDojo is not just a dataset; it is a complete open-source platform offering a suite of tools, models, and benchmarks to promote research in the academic community on large language model (LLM)-assisted theorem proving. By open-sourcing code and models, LeanDojo aims to lower the barrier to entry for machine learning research in theorem proving, providing reproducible benchmarks and a strong foundation for future research.

NuminaMath

https://huggingface.co/datasets/AI-MO/NuminaMath-CoT

{"source":"synthetic_math","problem":"        Consider the terms of an arithmetic sequence: $-\frac{1}{3}, y+2, 4y, \ldots$. Solve for $y$.","solution":"For an arithmetic sequence, the difference between consecutive terms must be equal. Therefore, we can set up the following equations based on the sequence given: \[ (y + 2) - \left(-\frac{1}{3}\right) = 4y - (y+2) \] Simplify and solve these equations: \[ y + 2 + \frac{1}{3} = 4y - y - 2 \] \[ y + \frac{7}{3} = 3y - 2 \] \[ \frac{7}{3} + 2 = 3y - y \] \[ \frac{13}{3} = 2y \] \[ y = \frac{13}{6} \] Thus, the value of $$y$$ that satisfies the given arithmetic sequence is $\boxed{\frac{13}{6}}$.","messages":[ { "content": "Consider the terms of an arithmetic sequence: $-\\frac{1}{3}, y+2, 4y, \\ldots$. Solve for $y$.", "role": "user" }, { "content": "For an arithmetic sequence, the difference between consecutive terms must be equal. Therefore, we can set up the following equations based on the sequence given:\n\\[ (y + 2) - \\left(-\\frac{1}{3}\\right) = 4y - (y+2) \\]\n\nSimplify and solve these equations:\n\\[ y + 2 + \\frac{1}{3} = 4y - y - 2 \\]\n\\[ y + \\frac{7}{3} = 3y - 2 \\]\n\\[ \\frac{7}{3} + 2 = 3y - y \\]\n\\[ \\frac{13}{3} = 2y \\]\n\\[ y = \\frac{13}{6} \\]\n\nThus, the value of $$y$$ that satisfies the given arithmetic sequence is $\\boxed{\\frac{13}{6}}$.", "role": "assistant" } ]}

The NuminaMath dataset is a groundbreaking initiative that aggregates 860,000 problem-solution pairs from various math competitions, forums, and educational resources to advance artificial intelligence capabilities in the field of mathematics. The construction process of this dataset involves a wide range of sources, including MATH, GSM8K, AMC, AIME, and the application of technologies such as OCR, translation, refinement, and Chain-of-Thought (CoT) formatting. The NuminaMath dataset is not only large in scale but also supports chain-of-thought reasoning through its meticulously designed CoT format, which is crucial for training large language models (such as GPT-4) to solve complex mathematical problems. The successful application of this dataset is evident in its fine-tuning of models that won the AIMO Progress Prize, demonstrating its effectiveness in enhancing AI mathematical reasoning capabilities. The creation and utilization of the NuminaMath dataset mark a significant step forward for artificial intelligence in mathematical education and technical challenges.

DART-Math

https://github.com/hkust-nlp/dart-math

{"query":"Let \[f(x) = \left\{ \begin{array}{cl} ax+3, &\text{ if }x>2, \\ x-5 &\text{ if } -2 \le x \le 2, \\ 2x-b &\text{ if } x <-2. \end{array} \right.\]Find $$a+b$$ if the piecewise function is continuous (which means that its graph can be drawn without lifting your pencil from the paper).","response":"For the function to be continuous, the parts of the piecewise function must meet at $$x = 2$$ and at $x = -2$. This means that at $x = 2$, $$ax + 3 = x - 5$$ and at $x = -2$, $x - 5 = 2x - b$. From $ax + 3 = x - 5$, we get $ax - x = -8$, so $(a-1)x = -8$, and $$x = 2$$ to get $(a-1)2 = -8$. Solving $$(a-1)2 = -8$$ for $$a$$ gives us $2a - 2 = -8$, so $2a = -6$, and $a = -3$. From $x - 5 = 2x - b$, we get $-5 - 2x = -b$, or $-5 - 2(-2) = -b$, $since x = -2$. Thus, $-1 = -b$, so $b = 1$. The problem asks for $a + b$, so $-3 + 1 = -2$. The answer is: $$2$$ $-2$"}

The DART-Math dataset is a synthetic dataset specifically designed to enhance the capabilities of large language models in solving mathematical problems. It is generated using the Difficulty-Aware Rejection Tuning (DART) method, which places special emphasis on challenging problems by allocating more generation attempts to them, thereby ensuring a greater number of training samples for difficult mathematical questions. The DART-Math dataset contains approximately 590,000 examples, which is smaller than previous datasets, but its design and generation strategy significantly improve the model's ability to handle challenging problems. The dataset was created using only the 7B-parameter open-source model DeepSeekMath-7B-RL, without relying on larger proprietary models like GPT-4. By fine-tuning base models ranging from 7B to 70B parameters, a series of models named DART-Math were produced. These models significantly outperform traditional rejection fine-tuning methods on six mathematical benchmarks, including MATH and GSM8K, and even surpass state-of-the-art techniques in some tests, despite using a smaller dataset and non-proprietary models. Therefore, the DART-Math dataset has proven to be a highly effective and cost-efficient public resource for improving mathematical problem-solving capabilities.

DeepSeekMath

Although DeepSeekMath has not open-sourced its dataset, it provides a pathway for generating high-quality mathematical datasets.

DeepSeekMath Dataset Generation Process

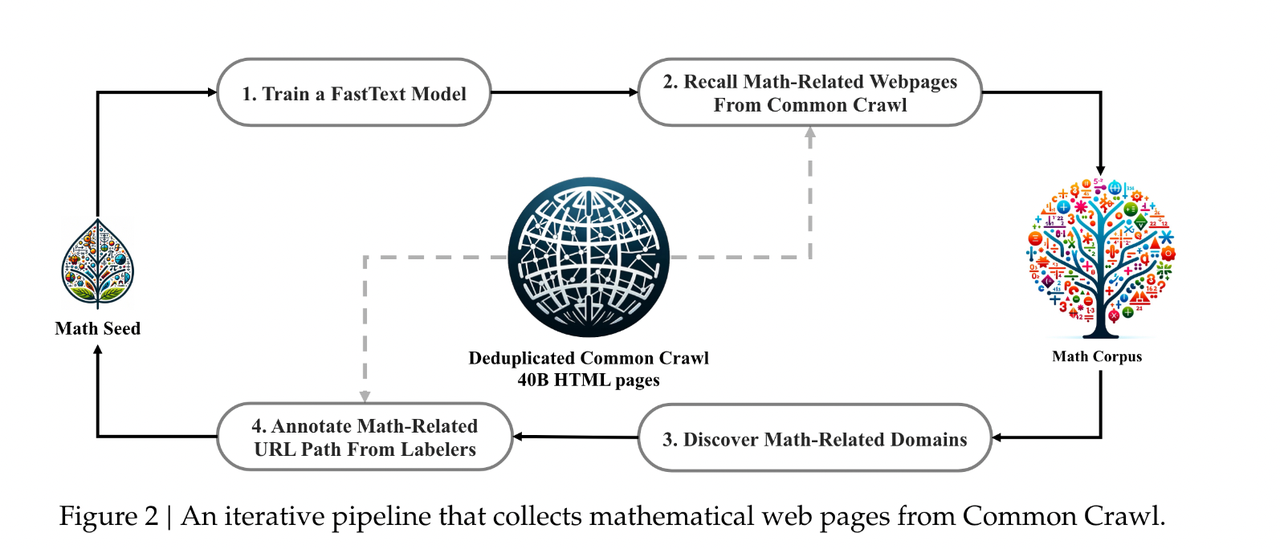
• Data Source: The dataset construction begins with the Common Crawl project, a dataset containing copies of web pages updated monthly. Leveraging this vast data source, a large amount of potential math-related content can be extracted.
• Initial Screening Process: To filter out math-related content, the research team first built a seed dataset from OpenWebMath. They used this seed dataset to train a fastText model for identifying and retrieving more math-related web pages.\
• Classification and Filtering: The trained fastText model was applied to the Common Crawl dataset to classify and filter pages, retaining only those related to mathematics. This process involved multiple iterations to ensure the model could continuously identify more math-related content from Common Crawl.
• Dataset Scale: After several iterations, 35.5 million math-related web pages were collected, containing a total of 120 billion math-related tokens. This massive dataset serves as raw material for further training of language models.
• Deduplication and Screening: To ensure data quality, the raw data underwent deduplication. Additionally, to avoid contamination of training data with test or validation sets, pages matching evaluation benchmarks were excluded.
• Iterative Optimization: Throughout the dataset construction process, the research team continuously iterated and optimized the data filtering model to ensure the dataset's diversity, coverage, and quality. The final DeepSeekMath dataset exhibits high mathematical relevance, providing rich training materials for language models in mathematical reasoning.

After four rounds of iteration, a corpus containing 35.5 million math-related web pages and 120 billion math-related tokens was compiled. During this process, to avoid benchmark contamination, web pages matching evaluation benchmarks were excluded. Furthermore, the quality of the DeepSeekMath dataset was validated through comparisons with other datasets such as MathPile, OpenWebMath, and Proof-Pile-2, demonstrating its advantages in high quality, multilingual content coverage, and large scale. It has shown significant contributions to improving performance in downstream mathematical reasoning tasks.

AlphaProof

Google's DeepMind team released a technical sharing on AlphaProof, which, together with AlphaGeometry, solved 4 problems from this year's IMO (International Mathematical Olympiad), achieving a performance equivalent to a silver medal.

AlphaProof Reinforcement Learning Training Cycle Flowchart

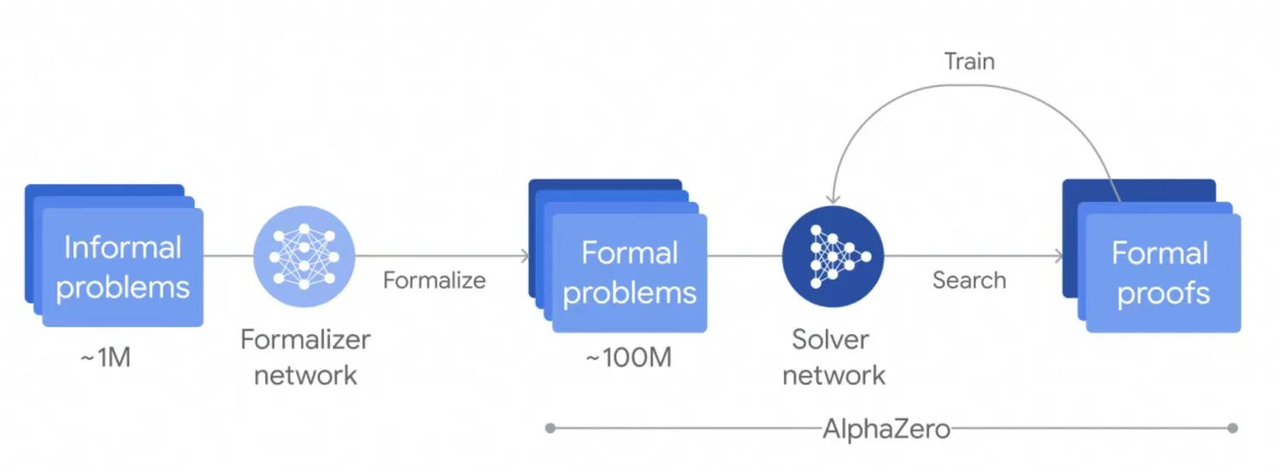
The process of generating the dataset for training the AlphaProof model begins with using the pre-trained Gemini language model as the foundation. This model is fine-tuned to automatically convert natural language descriptions of mathematical problems into statements in Lean formal language, thereby creating a large library of formal mathematical problems at varying difficulty levels. The AlphaProof system then generates solution candidates for these problems and searches for possible proof steps in Lean to prove or refute these candidates. Each discovered and validated proof is used to reinforce AlphaProof's language model, enhancing its ability to solve more challenging problems. In the weeks leading up to the IMO competition, AlphaProof underwent extensive training by proving or refuting millions of problems covering a wide range of difficulties and mathematical topics. More importantly, this training process continued during the competition, with the model being continuously reinforced by proving self-generated variants of competition problems until complete solutions were found. This process ingeniously combines natural language processing, formal mathematical reasoning, and reinforcement learning to create a self-improving mathematical problem-solving system.