This article explains why the Direct Comparison Test is one of the most powerful, intuitive tools for determining convergence of complex series and how the same logic applies when evaluating LLM system performance, particularly when comparing scaling laws, error curves, or benchmark score trajectories.
Why Direct Comparison Test Solves Complex Series!
Why Direct Comparison Test Solves Complex Series!
What Is the Direct Comparison Test?
The Direct Comparison Test evaluates convergence using bounding.
Given two series:
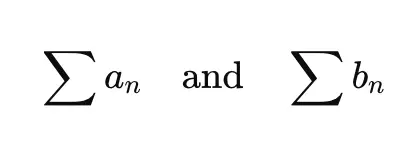
If, for all sufficiently large n:
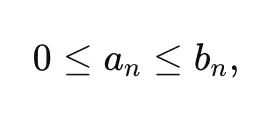
then:
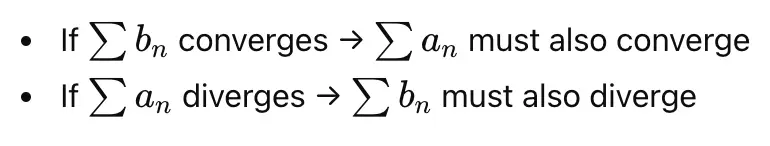
This relies on a simple observation:
If a smaller quantity adds up to infinity, the larger one must also diverge.
If a larger quantity adds up to a finite value, the smaller one must also converge.
That’s the entire logic.
Why the Direct Comparison Test Makes Hard Problems Easy
The DCT shines when a series looks complicated, but the dominant term is obvious.
Instead of using advanced tests (Ratio, Root, Integral), you only need to:
✔ identify the dominant term
✔ match it to a known “template series”
✔ apply bounding logic
Common benchmarks:

If you can find a clean upper or lower bound, the conclusion follows immediately.
Why It Maps Surprisingly Well to LLM Benchmarking
Unexpectedly, the same reasoning behind the Direct Comparison Test also appears in LLM benchmarking and model evaluation.
When evaluating a new large language model, researchers often examine:
- Loss curves
- Benchmark accuracy
- Scaling laws
- Error decay
- Performance plateaus
These curves are interpreted through comparison, not isolation.
➤ This is exactly how the Direct Comparison Test works.
You understand a new behavior by relating it to a known baseline.
Series Comparison ↔ Model Comparison
| Direct Comparison Test | LLM Benchmarking |
|---|---|
| Compare unknown series to known convergent/divergent series | Compare new model curves to established models |
| Determine long-term behavior | Determine performance limits or plateaus |
| Bound one sequence by another | Bound performance relative to a baseline |
| “Does this grow faster or slower?” | “Does this model improve faster or slower?” |
The underlying principle is the same:
To understand a complex pattern, compare it to a familiar one.
A Visual Analogy
Imagine two LLM loss curves during training:
- A known baseline curve (like LLaMA or GPT series)
- A new model’s curve
If the new curve always lies below the baseline (lower loss), then you instantly know:

This mirrors:
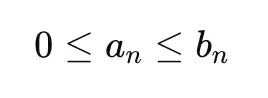
Just as LLM researchers conclude that one model performs consistently better, mathematicians conclude that a series follows the convergence behavior of its comparison partner.
The analogy makes the DCT far more intuitive, especially for visual learners.
Practical Examples Where DCT Shines
Example 1: Rational expressions
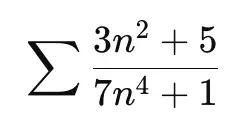
Dominant behavior:
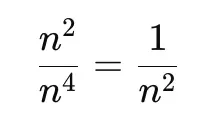
Since p-series with p = 2 converges:
→ The original series converges.
Example 2: Polynomial vs exponential
Exponential dominates polynomial:
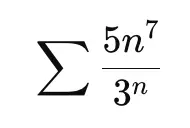
Geometric series converges:
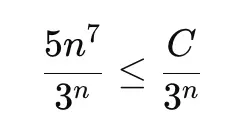
→ This series converges.
Example 3: Demonstrating divergence
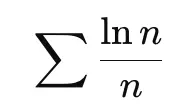
Since:
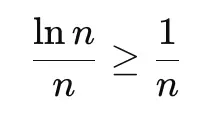
And the harmonic series diverges:
→ The original series diverges.
When to Use the Direct Comparison Test
Use DCT when:
✔ The dominant term is clear
✔ Terms remain non-negative
✔ The series resembles a known p-series or geometric series
✔ Other tests seem unnecessarily complicated
Typical patterns:
- 1/{n^p} with extra numerators
- logarithms mixed with powers
- polynomials over exponentials
- combined expressions that simplify at large nnn
If you can bound it, you can solve it.
Conclusion: The Power of the Direct Comparison Test
- Fast and intuitive
- Works on many types of series
- Gives guaranteed answers when bounds hold
- Avoids complex algebra
- Builds on familiar benchmark behavior
- Shares the same logic as comparing performance curves in modern machine learning
The Direct Comparison Test is one of the most accessible and powerful tools for handling infinite series, making even the toughest problems feel manageable.